ATCO - Optimized Scheduling
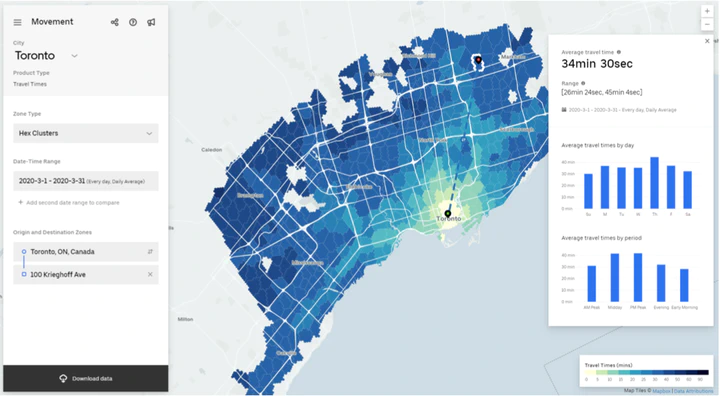 Fig. 1: “Uber Movement” data for Toronto in March 2020
Fig. 1: “Uber Movement” data for Toronto in March 2020Optimization of Employee Work Schedule,
Industry mentors: Vakhtang Putkaradze and Kui Pan
Due to the outbreak of COVID-19 around the world, and government policies implemented as a response to the outbreak, many corporations have chosen to let their employees work from home to prevent the spread of the disease. In order to safely re-open the economy, one of the recommendations from health authorities is to allow only a limited percentage of workers in the workplace at any specific time. Given these constraints, it is useful for companies to arrange flexible work schedule so the employees go to offices during reasonable working hours, and at the same time reduce their commute time to improve their productivity. In this problem, you will help a model business to design and optimize their employees’ working-at-office schedule using a combination of criteria which you deem to be important, and real-life data such as traffic, limitation on work schedule hours, commuting time and others.
Problem Description
For a company in a given city, the known parameters include: the total number of employees $N$, the location of the company $S$ , the home address of each employee $S^i_e (1 \leq i \leq N)$, the maximum percentage of workers allowed at the office \alpha, the reasonable working hours (a time window, or distribution of weights indicating less/more desirable), a minimum number of hours for each employee to work at office per week $T$, and the historical traffic pattern of the city. For simplicity, you can assume that there are no specific working sub-groups that have to be present at a given time (e.g., incorporating meeting schedule). Since this is an open question, the schedule of employees’ working at the office can be optimized with respect to different aspects, such as the commute time between office and home, road safety conditions (presence of ice/snow), traffic conditions, etc. You will be required to define the parameter (or parameters) to optimize and use quantitative methods to justify your conclusions.
Data Sources
For this problem, you can choose your favorite city anywhere in the world (Calgary, Toronto, Seattle, New York, New Delhi, Mexico City…). We advise to take the model company location to be chosen downtown as it usually has more associated traffic data. The employee home address $S^i_e$ can be randomly sampled throughout the city. Some of the known parameters can be set as any reasonable values. For example: $N = 200\sim 1000$, $\alpha = 25\%\sim 35\%$, $T = 15\sim 25$ hours, and working time window $7\textrm{AM}− 7\textrm{PM}$ (or, alternatively, set your own weights in time desirability distribution). It is recommended for the participants to find their own datasets depending on the parameter chosen to be optimized. As an example, to optimize the commute time of employees some useful datasets are available, such as the “Uber Movement” 1 that has provided the historical travel time between two locations for a given period in each day (see Fig. 1), and the “Calgary Transit Reliability” 2.
Related Knowledge
There is no prerequisite knowledge strongly needed for this problem, but some level of knowledge in “Mathematical Optimization” 3 and “Optimization Algorithms” 4 are desired. One may also find the “Stochastic Gradient Descent” 5 frequently used in Deep Learning is useful here.
Evaluation Metrics
The final submission will be evaluated based on the following key metrics:
- Clear definition of optimization problem with the corresponding optimization parameter.
- Use appropriate algorithms, clean explanation of processes leading to the conclusion.
- Finding and use of reliable data sources, handle missing data correctly, list the origin and determine the accuracy of data.