Thoron testing

Industry Mentor: Kai Kaletsch, President, Environmental Instruments Canada

Residential radon progeny exposure is the second leading cause of lung cancer, after smoking. The two main radon isotopes are Rn-222, which is part of the uranium-238 decay chain, and Rn-220, also called thoron, which is part of the thorium-232 decay chain. There is currently much interest in the Rn-220 contribution to radon progeny exposure, which has so far been largely ignored. (Rn-220 has a relatively short half life and usually decays before it reaches the living areas in a house and it usually doesn't show up in radon measurements. But, Rn-220 has a longer lived decay product which does reach living areas and contributes to radon progeny exposure. It can even exceed the Rn-222 contribution.)

Environmental Instruments Canada (EIC) produces a Radon Sniffer (see https://radonsniffer.com/), which is used by radon mitigators and building scientists to find radon entry points. These sniffers currently assume all radon is Rn-222. See the appendix for a more detailed description of how the sniffer works. We want to extend the functionality to Rn-220. 

Overview

The sniffer has a pump that draws in air. The air is filtered, only passing radon (a noble gas) and filters radon progeny. The sniffer counts alpha particles and can not distinguish between alpha particles from the decay of  Rn-222, Rn-220 or their progeny. One method of determining the ratio of Rn222/Rn220 in the air is by implementing sampling and counting sequences and observing the change in alpha count rate over time.

The relevant part of the decay chains for the isotopes are Rn220(54.5 sec half-life)->Po216(0.158 sec half-life)->Pb212(10.6 hour half-life) etc and Rn222(3.825 day half-life)->Po218(3.05 min half-life)->Pb214(26.8 min half-life) etc. There are more progeny in each series. But, to first order, these can be ignored and will be for this example.

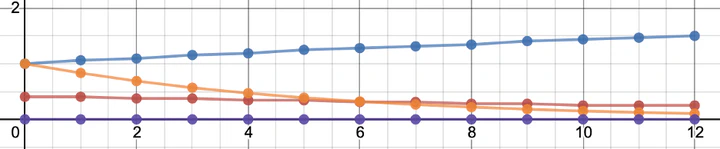
In the following graph, the blue line shows the count rate over time after the sniffer is filled with Rn222. Each time interval is 15 seconds and 12 intervals correspond to 3 minutes. Conceptually, this can be understood like this: Rn-222 has an almost 4 day half life. So, over 3 minutes, it’s activity is essentially constant. Each Rn-222 decay produces a Po-218 (also an alpha emitter), which grows in over time to 50% of the parent’s activity after 1 Po-218 half life.

The orange line shows the count rate over time after the sniffer is filled with Rn220. Rn220 decays with a 1 minute half life. So, after 3 minutes, there is only 1/8 of the original activity left. Rn-220 decays into Po216, which has a fraction of a second half life. I.e., it decays as soon as it is created and we don’t have to model it separately. We simply observe 2 alpha particles for each Rn220 decay. 

One method of determining the ratio of Rn222/Rn220 would be to fill the cell, stop the pump, and compare the number of counts in the first 15 seconds (interval 0 to 1) to the number of counts in interval 11 to 12 (seconds 165 to 180). If the count rate increases, we had mostly Rn222 and, if it decreases, it was Rn220.

A second method would be to re-start the pump after 3 minutes to flush out any radon (say for 1 minute). The radon progeny attaches to the side of the cell and does not flush out. The red line in the graph above shows the expected count rate over time in the Rn222 scenario. I.e. the Rn-222 is gone but there is still some Po218 plated out, which continues decaying with a 3 minute half life. If the air initially only contained Rn-220, it will be all flushed out and there will be no more counts (purple line). So, we could confirm our Rn222/Rn220 ratio calculation by counting after the cell has been purged.

The Problem

In the above example, we only count for 15 seconds. That might not be enough to get good counting statistics. We also ignore all counts that are received between point 1 and point 11. That is a waste of good data. The problem is to develop an optimized sampling and counting sequence that results in the best statistical accuracy. (e.g. count continually and fit the cumulative number of counts to some curve???).

That is the simplified problem statement. There are some complicating factors: Unless this is done with a perfectly clean detector, there will be background activity in the cell, which changes over time. (This is from the isotopes further down the decay chain, which we have ignored so far.)

Required Qualifications

The concept of radioactive decay and half life is first year physics. Being able to write (and understand) the coupled differential equations describing a decay series is more advanced. But, we deal with this all the time and can provide the numerical models.

The input we are seeking from the participants is to optimize the sampling and counting sequence that results in the best statistical accuracy. This is a statistics problem.

The problem can be modelled on a spreadsheet and will not require any coding. Our app developer will be available to code the sampling/counting sequences and analysis method developed by the participants and their solutions can be tested almost immediately.

I will be around to provide input from the physics/technology side.

Open Endedness

Solving the problem, as detailed above, would be the first step. However, we are definitely open to other, creative solutions. For example, could we just continue counting after the day's samples are all completed and the cell is flushed and calculate the ratio of Rn222/Rn220 by observing the decrease in count rate over time? (That will be driven by the longer lived progeny, which we have ignored so far.) Maybe we can even correct the radon sniffer algorithm, in real time, as continuous samples are taken and we don't need a dedicated thoron sampling sequence. We would do that by identifying count rate curves that would be impossible if we sample only Rn-222. There are a few options that can be explored after the initial problem is solved.